右手系

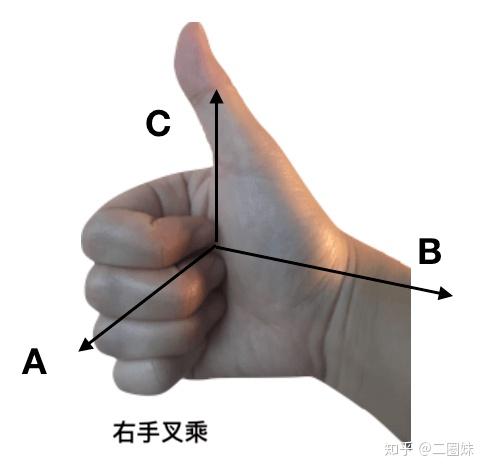
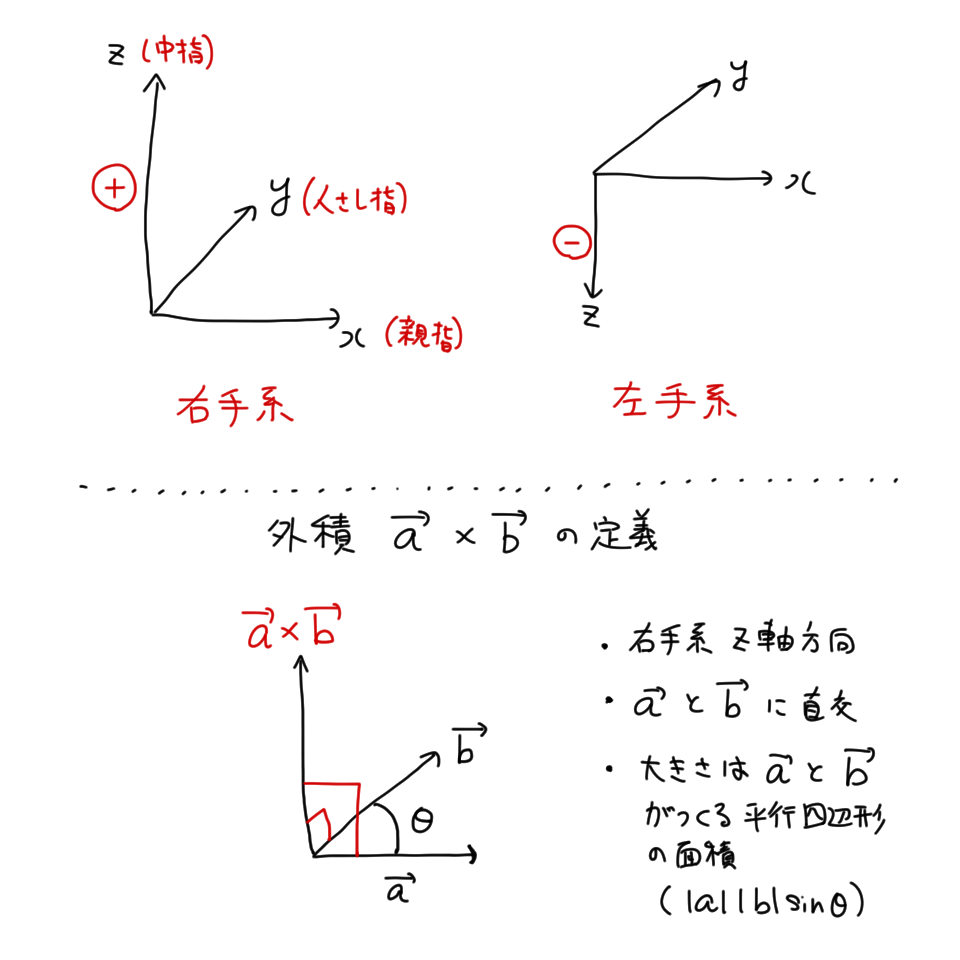
右手系（みぎてけい、英: right-handed system）または正系（せいけい、positive-oriented system）は、線型代数学における座標系で、右手の法則（right-hand rule）に従うものを指し、左手系と区別される。多くの分野では右手系が標準とされるが、測量の分野では左手系が標準である。

右手系・左手系という性質は、直交座標系とは限らない座標系に対しても考えられる。より抽象的には、順序付けられた基底に対して定義される。また、3次元に限らず、2次元以上の任意の次元のユークリッド空間に対しても定義される。

定義

n ≥ 2 とする。n 次元ユークリッド空間 Rⁿ において、j 番目の座標が 1 でその他が 0 であるベクトルを、e_j と表すこととする。<e₁, …, e_n> は、Rⁿ の標準的な基底である。任意に2通りの基底 A := <a₁, …, a_n> と B := <b₁, …, b_n> を取ったとき、その間の変換行列は正則行列となる。その行列式が正であるときに A と B は同値であるとして同値関係を定義すると、基底全体の集合はちょうど2つの同値類に類別される。標準的な基底と同値である基底は右手系であるといい、同値でない基底は左手系であるという。

性質

標準的な基底は右手系である。
<a₁, …, a_n> が右手系であるとき、その中の2つのベクトルの順序を入れ替えたもの、例えば <a₂, a₁, a₃, …, a_n> は左手系になる。より一般に、n 次対称群の元 σ に対し、<a_σ(1), …, a_σ(n)> が右手系であることと、σ の符号が 1 であることは同値である。
基底 A = <a₁, …, a_n> に対し、n 次正方行列 (a₁, …, a_n) の行列式が正ならば A は右手系であり、負ならば左手系である。

一般のベクトル空間

V を R 上の n 次元ベクトル空間とする。Rⁿ の場合と同様に、V の基底全体の集合も、2つの同値類に類別される。そのどちらの元を右手系と呼び、どちらの元を左手系と呼ぶべきかは自然には定まらない。同型写像 φ Rⁿ → V をひとつ定めたならば、<φ(e₁), …, φ(e_n)> と同値である基底を右手系と呼ぶことはできる。