三焦点テンソル

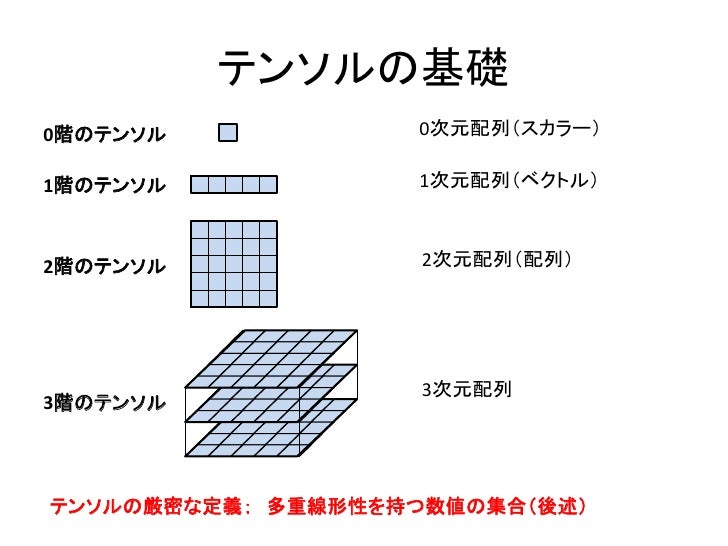
三焦点テンソル（さんしょうてんテンソル、英:trifocal tensor, tritensor）、または三重焦点テンソル（さんじゅうしょうてんテンソル）は、コンピュータビジョンの分野で用いられる3つのビュー間のすべての射影幾何学的関係を組み込んだ3×3×3の数値配列（テンソル）である。これは、3つのビュー内の対応する点または線の座標を関連付ける。シーン構造とは無関係であり、3つのビュー間の相対的な動き（ポーズ）とそれらの固有のキャリブレーションパラメーターのみに依存する。したがって三焦点テンソルは基礎行列を3つのビューに拡張したものとみなせる。テンソルは27個の要素で構成されているが、実際にはそのうちの18個だけが独立している。

いわゆるキャリブレーションされた三焦点テンソルも存在する。これは、3つのビューの点と線の座標を固有のパラメーターに関連付け、カメラの相対的な姿勢をグローバルスケールも含めて構成し、計11 の独立した要素（自由度）を表す。自由度の減少は非線形性の増加を犠牲にしてと、推定に使用する対応の数を減らすことができる。

相関スライス

テンソルは、その相関スライス（英 : correlation slices）として知られる3つのランク2の 3 x 3 行列${\displaystyle {\mathbf {T} }_{1},\;{\mathbf {T} }_{2},\;{\mathbf {T} }_{3}}$の集合とみなすこともできる。3つのビューの射影行列が${\displaystyle {\mathbf {P} }=[{\mathbf {I} }\;|\;{\mathbf {0} }]}$、${\displaystyle {\mathbf {P} }'=[{\mathbf {A} }\;|\;{\mathbf {a} }_{4}]}$、${\displaystyle {\mathbf {P} ''}=[{\mathbf {B} }\;|\;{\mathbf {b} }_{4}]}$ であると仮定すると、対応するテンソルの相関スライスは${\displaystyle {\mathbf {T} }_{i}={\mathbf {a} }_{i}{\mathbf {b} }_{4}^{t}-{\mathbf {a} }_{4}{\mathbf {b} }_{i}^{t},\;i=1\ldots 3}$のように閉じた形式で次のように表現できる。ここで${\displaystyle {\mathbf {a} }_{i},\;{\mathbf {b} }_{i}}$はそれぞれカメラ行列のi番目の列である。ただし実際には、このテンソルは3つのビューにわたる点と線の一致から推定される。

三重線形拘束条件

三焦点テンソルの最も重要な特性の1つは、3つの画像の線と点の間に線形関係が生じることである。より具体的には、対応する点の3つ組を${\displaystyle {\mathbf {x} }\;\leftrightarrow \;{\mathbf {x} }'\;\leftrightarrow \;{\mathbf {x} }''}$、それらを通る対応する直線を${\displaystyle {\mathbf {l} }\;\leftrightarrow \;{\mathbf {l} }'\;\leftrightarrow \;{\mathbf {l} }''}$としたとき、次の三重線形拘束条件（英 : trilinear constraints）に従う。

${\displaystyle ({\mathbf {l} }^{\prime t}\left[{\mathbf {T} }_{1},\;{\mathbf {T} }_{2},\;{\mathbf {T} }_{3}\right]{\mathbf {l} }'')[{\mathbf {l} }]_{\times }={\mathbf {0} }^{t}}$

${\displaystyle {\mathbf {l} }^{\prime t}\left(\sum _{i}x_{i}{\mathbf {T} }_{i}\right){\mathbf {l} }''=0}$

${\displaystyle {\mathbf {l} }^{\prime t}\left(\sum _{i}x_{i}{\mathbf {T} }_{i}\right)[{\mathbf {x} }'']_{\times }={\mathbf {0} }^{t}}$

${\displaystyle [{\mathbf {x} }']_{\times }\left(\sum _{i}x_{i}{\mathbf {T} }_{i}\right){\mathbf {l} }''={\mathbf {0} }}$

${\displaystyle [{\mathbf {x} }']_{\times }\left(\sum _{i}x_{i}{\mathbf {T} }_{i}\right)[{\mathbf {x} }'']_{\times }={\mathbf {0} }_{3\times 3}}$

ここで${\displaystyle [\cdot ]_{\times }}$は、交代外積行列を意味する。

移送

3つのビューの三焦点テンソルと2つのビューの対応する点のペアが与えられたとき、3番目のビューの点の位置をそれ以上の追加情報なしで決定することができる。これは点移送（英 : point transfer）として知られており、線分と円錐曲線にも同様の移送が可能である。一般の曲線の場合、移送は接触円（曲率）の局所微分曲線モデルを通じて実現でき、円錐曲線として移送できる。 キャリブレーションされた三焦点テンソルを使用した空間の歪みを反映する3次モデルの移送は研究されているが 、キャリブレーションされていない三焦点テンソルについては未解決の問題が残っている。

推定

キャリブレーションされていない場合

古典的なケースは、3つの解を与える6点対応 である。

9線対応から三焦点テンソルを推定するケースは、最近解決されたばかりである。

キャリブレーションされている場合

キャリブレーションされた三焦点テンソルを推定することは、非常に難しいとされており、4点対応が必要である。

3点のみの対応を使用するケースが最近解決された。この場合、点は接線方向または入射線に関連付けられる。入射線を持つ点が2つだけの場合、これは次数312の最小化問題であり（従って最大で312の解が存在する可能性がある)、各点に接線を持つ一般の曲線や方向性（SIFT方向等）を持った特徴点の場合に適している。同じ手法で3つの点の対応と1つの線の対応が混在する場合も解決され、次数216で最小であることも示されている。

脚注

参考文献

• Hartley, Richard I. (1997). “Lines and Points in Three Views and the Trifocal Tensor”. International Journal of Computer Vision 22 (2): 125–140. doi:10.1023/A:1007936012022. 
• Torr, P. H. S.; Zisserman, A. (1997). “Robust Parameterization and Computation of the Trifocal Tensor”. Image and Vision Computing 15 (8): 591–607. doi:10.1016/S0262-8856(97)00010-3. 

外部リンク

• 三焦点幾何学の可視化（元はINRIA Robotvis の Sylvain Bougnoux によるもので、Javaが必要）

アルゴリズム

• キャリブレーションされていない 3 焦点テンソル推定のMatlab実装と基礎行列との比較
• 最適化されたホモトピー連続コードを利用したキャリブレーションされた三焦点テンソル推定の C 実装。現在、3つの対応点とこれらの点での線（特徴点の位置と向き、または接線を持つ曲線点など）の場合と、3つの対応点と1つの線の対応の場合が含まれる。